Для определения индексов Миллера необходимо:

• найти точки пересечения плоскости кристаллической решетки с осями координат;
• перевести результат в единицы постоянных решетки , , ;
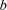• взять обратные значения полученных чисел и привести их к наименьшему целому, кратному каждого из чисел.

Результат, заключенный в круглые скобки (), и представляет собой индексы Миллера данной плоскости кристалла.

Например, если плоскость пересекает оси в точках с координатами 1, 2, 3 (рис. а), то обратные им числа будут 1, 1/2, 1/3, а наименьшие целые числа, имеющие те же отношения, соответственно 6, 3, 2, т. е. индексы Миллера для этой плоскости — (632). Если плоскость параллельна одной из осей, то точка пересечения с этой осью принимается за бесконечность, а соответствующий индекс — за ноль. Если плоскость пересекает ось в области отрицательных значений, то соответствующий индекс будет отрицательным. Для указания этого над индексом помещается минус: (). В качестве примера на рис. б приведены индексы Миллера некоторых наиболее важных плоскостей кубического кристалла.